Compound Interest
Compound Interest occurs when interest is added to the principal every period.
The period varies, like yearly, quarterly, monthly, etc...
In a monthly compounded interest rate, the interest is added to the balance every month.
For example: if you deposit $1000 in an account that earns 1% interest per month:
- The first month you would earn $10 (1000 x 0.01), total balance= $1010
- Your second month you would earn $10.1 (1010 x 0.01), total balance = $1020.1
- Your third month you would earn $10.201 (1020.1 x 0.01), total balance = $1030.301
The effect of compounding depends on the frequency with which interest is compounded and the periodic interest rate which is applied. Therefore, in order to define accurately the amount to be paid under a legal contract with interest, the frequency of compounding (yearly, half-yearly, quarterly, monthly, daily, etc.) and the interest rate must be specified. Different conventions may be used from country to country, but in finance and economics the following are common
definitions:
- Periodic rate: the interest that is charged (and subsequently compounded) for each period, divided by the amount of the principal. The periodic rate is used primarily for calculations, and is rarely used for comparison.
- The nominal annual rate or nominal interest rate is defined as the periodic rate multiplied by the number of compounding periods per year. For example, a monthly rate of 1% is equivalent to an annual nominal interest of 12%.
- Effective annual rate: this reflects the effective rate as if annual compounding were applied: in other words it is the total accumulated interest that would be payable up to the end of one year.
Formulas:
- Future Value, the value of money invested now afer a period of time
FV = PV(1+i)n
FV= Future Value, PV= Present Value, i= fixed interest rate, n= period
- Present Value, how much do I invest now to end up with a certain amount
PV = FV / (1+i)n
- Mortgage Payments, The interest on U.S. mortgages is compounded monthly
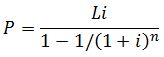
Where n= number or months, L= principal or loan amount, i= monthly percentage
rate : if your APR is 5%, then i = (0.05/12)